top of page

LSTM

מבוא

מאמר זה בא להדגים שימוש במודל LSTM בעזרת ספריות Tensorflow & Keras ב- Python.

מודל LSTM בנוי מרשת ניורונים הלומדת ולבסוף משערכת נתונים בהסתמך על נתונים היסטורים.

לא נתמקד כאן במתמטיקה שמאחורי המודל, אך עם זאת חשוב להבין מהי רשת ניורונים בסיסית

ואת אופן פעולתה לפני קריאת התוכן. 

​

במה כן נתמקד ?​

  • ולידציה והערכת ביצועים.

  • שיקולים בהרכבת המודל.

  • כתיבת קוד ב-python.

הערכת ביצועים

שני הפקטורים העיקריים אליהם נתייחס באומדן המודל הם Overfitting ו- RMSE.

​

  • Overfitting - מצב מגמתי בו ערך פונקציית המחיר (MSE) של סט הולידציה כתלות במספר                              ה-epochs עולה על זה של הסט המאמן את המודל. במקרה כזה המודל יתן                                תוצאות טובות אם נזין אליו נתונים שהוא התאמן עליהם ותוצאות עלובות כאשר                            נזין אליו נתונים שהוא עוד לא ראה.   

                           בתמונה ניתן לראות שהמודל עבור סט הולידציה הראשון נמצא ב-Overfitting                                   בעוד עבור הסט השני, אמנם קיימת שגיאה אך היא יותר יציבה וקבועה.

​

overfitting.png

​

  • RMSE -  שורש השגיאה הריבועת הממוצעת בין הערכים האמיתיים לבין התחזיות. 

                    הכלי העיקרי באומדן המודל בין השיטות שונות אותן נפרט בהמשך.

שיקולים בהרכבת המודל

קיימות מספר אפשרויות שונות לשערוך הנתונים, דבר הבא לידי ביטוי בהרכבת המודל.​

זהו שלב שמצריך להרכיב את המודל כל פעם בצורה אחרת ותלוי בעיקר בצרכי המשתמש,

כמות הנתונים העומדים לרשותו ושיקולי זמן.

 

האפשרויות השונות להרכבת המודל:

  1. שערוך label בודד כתלות ב-feature בודד.

  2. שערוך label בודד כתלות במספר features.

  3. שערוך מספר labels כתלות ב-feature בודד.

  4. שערוך מספר labels כתלות במספר features.

​

כמו כן ישנה גישה נוספת אשר מתבססת על שערוך label כתלות בשערוך label קודם

והיא איננה מצריכה בבניית מודל חדש. 

​

בחירת המודל הרצוי צריכה להיות מהשיקולים הבאים :​                                                                 

​

  1. דיוק - אין ספק שזה הגורם המשמעותי ביותר, בין אם המודל פשוט ובין אם הוא עמוס בסופו של דבר מה שחשוב הן התוצאות.                                                                                                                         

  2. זמן -  ככל שהמודל מתחשב במספר רב יותר של features כך גם יקח יותר זמן לאמן אותו דבר אשר לא בהכרח יוביל לשיפור השגיאה, כמו כן הגדלת מספר השכבות ברשת, כמות הניורונים בכל שכבה והקטנת כמות שורות הדאטה שנכנסות אל הרשת בכל פעם, כל אלה אולי ישפרו את המודל אך בהכרח המודל יתאמן יותר זמן.

​

קוד Python

  1.     import numpy as np

  2.     import pandas as pd

  3.     import matplotlib.pyplot as plt

  4. ​

  5.     base_path = "C:/Website_LSTM/"

  6.     df = pd.read_csv('f'{base_path}RSCCASN.csv',

  7.                   index_col='DATE',

  8.                   parse_dates=True)

  9. ​

  10.     days,length = 18,36

  11. ​

  12.     fig,ax = plt.subplots(figsize=(12,6))

  13.     ax.plot(df.index[:],df[:],label='train')

  14.     ax.plot(df.index[-days:],df[-days:],label='test') 

  15.     ax.set_xlabel('Date')

  16.     ax.set_ylabel('Millions of Dollars')

  17.     ax.set_title('Original Data')

  18.     plt.legend()

  19.     plt.grid()

  20.     fig.savefig(f'{base_path}Original Data.png')

 10.days - מספר החודשים אותם נשערך.   

      length - מספר החודשים הקודמים לחודש המשוערך מהם האלגוריתם לומד.

Original Data.png

 בתמונה ניתן לראות בכחול את הסט איתו נאמן את המודל ובכתום את הסט אותו ננסה לשערך ולחזות.

 הדאטה משקף את ההכנסות במילוני דולרים ממכירות בגדים בארה"ב בכל חודש בשנות 1992-2020.

 את הדאטה ניתן למצוא באתר https://fred.stlouisfed.org/series/RSCCASN

 ניתן לראות שיש לדאטה אופיין מחזורי ועבור חלק מהשנים המכירות פחות או יותר באותה הסקלה

 וזה חשוב כי כבר עכשיו ניתן לצפות שהמודל יתן תוצאות טובות אותן נאמוד בהמשך.   

  1.     train = df.iloc[:-days]

  2.     test = df.iloc[-days-length:]

  3.     from sklearn.preprocessing import MinMaxScaler

  4.     scaler = MinMaxScaler().fit(train)

  5.     train_sc, test_sc  = scaler.transform(train), scaler.transform(test)

 1. train - מורכב מכל חודשי הדאטה עד ה-18 החודשים האחרונים.

 2. test - מורכב מ 18+36 החודשים האחרונים של הדאטה הסיבה לכך היא ליצור סט ולידציה המורכב                  מ-18 דגימות ולא דגימה אחת אילו היינו לוקחים רק את ה-18 החודשים האחרונים.

 3-5. scaler - החלק הכי חשוב בנרמול הוא לנרמל רק על פי ערכי הסט המאמן ולהמיר את ערכי סט                          הולידציה אל אותה הסקלה. דבר זה מבטיח שאין למודל שום ידע קודם על סט הולידציה.

 דבר נוסף שחשוב לציין, אם כל הדאטה לא היה פחות או יותר באותה סקלה כמו למשל במחירי מניות   התוצאות היו רעות מהסיבה שמודל לא באמת יכול ללמוד כי אין שם שום נתונים היסטורים שחוזרים על   עצמם רק טווח הסקלה ממש גדול.

  1.     X_train,y_train = [],[]

  2.     for i in range(length,len(train_sc)):

  3.         X_train.append(train_sc[i-length:i,0])

  4.         y_train.append(train_sc[i,0])

  5.     X_train,y_train = np.array(X_train),np.array(y_train)

  6.     X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))

  7. ​

  8.     X_test , y_test  = [], []

  9.     for i in range(length,len(test_sc)):

  10.         X_test.append(test_sc[i-length:i,0])

  11.         y_test.append(test_sc[i,0])

  12.     X_test,y_test = np.array(X_test),np.array(y_test)

  13.     X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))

 1-4. יצירת סט אימון המורכב מדגימות של 36 חודשים הקודמים לחודש נוכחי, בעוד סט הטסט מורכב            מכל החודשים הנוכחיים להם יש דגימה בסט האימון.

        דוגמא מוחשית:

ex__x_train.PNG

 5-6 - המודל בהמשך מקבל מערך מסוג numpy בעל 3 מימדים (פיצרים,אורך דגימה,מספר הדגימות)

         ולכן יש צורך לעצב אותו למימדים הרצויים.

 8-13 - חוזרים על התהליך עבור סט הולידציה.

  1.     from tensorflow.keras.models import Sequential

  2.     from tensorflow.keras.layers import LSTM, Dense

  3.     from sklearn.metrics import mean_squared_error

  4. ​

  5.     model = Sequential()

  6.     model.add(LSTM(100,activation='relu',input_shape = (length,1)))

  7.     model.add(Dense(1))

  8.     model.compile(optimizer='adam',loss='mse')

  9. ​

  10.     epochs = 150; batch_size = 32;

תהליך בניית המודל:

 5. - Sequential - אובייקט עבור רשת שכל הניורונים בכל שכבה מחוברים לכל הניורונים בשכבה

                          הבאה.

 6. השכבה החבויה הראשונה ברשת (במקרה זה גם האחרונה) המורכבת ממאה ניורונים שלכל אחד 

     מהם יש פונקציית אקטביזציה לינארית. עבור השכבה החבויה הראשונה יש לציין את שני המימדים

     האחרונים של מערך ה-numpy שנכנס בשכבת ה-input הקודמת והם אורך הדגימה (36 חודשים) 

     וכמות הפיצרים. במקרה שלנו יש רק פיצר אחד שהוא גם הלייבל שאותו נרצה לחזות.

 7. שכבת המוצא ברשת המורכבת מניורון אחד.

 8. loss - פונקציית המחיר איתה נשאף לאפס את השגיאה.

     optimizer - סוג הגרדיאנט / שיטת חישוב בתהליך ה-Backpropagation לשקלול המשקלים       

                      ברשת.

 10. epochs - מספר הפעמים שנאמן את המודל בהם נכניס את כל הדגימות של סט האימון.

       batch_size - מסך כל הדגימות של סט האימון עבור epoch אחד,

                           מספר הדגימות (נבחר בצורה רנדומלית) שמחשבות את פונקציית המחיר

                           ונותנות משקל עדכני לרשת. 

 

      זהו השלב הקריטי בקוד, כאן צריך להתחשב בשיקולי זמן בבניית הרשת.

      שכן אם נוסיף שכבות חבויות נוספות, נעלה את מספר ה-epochs, נוריד את כמות ה-batch כל אלה        יעמיסו על המודל ויקח יותר זמן לאמן את הרשת.

      בחירת פונקציית אקטביזציה ואופטימייזר הם שיקולים הנובעים מהצורך שלנו בהתחשב בדאטה.   

  1.     loss = pd.DataFrame(index=list(range(1,epochs+1)),

  2.                         columns=[['Mse train','Mse Val','Real Rmse']])

  3.     loss.index.name = 'Epoch'

  4. ​

  5.     val_forecast_1_day = pd.DataFrame(index=df.index[-days:],

  6.                                       columns=[f'Epoch {i}' for i in range(1,epochs+1)])

  7. ​

  8.     for i in range(1,epochs+1):

  9.         print(f'Epoch {i}.')

  10.         model.fit(X_train, y_train, 

  11.                        batch_size = batch_size,

  12.                        validation_data=(X_test, y_test))

  13.         train_mse,val_mse = model.history.history.values()

  14.         loss.iloc[i-1,0],loss.iloc[i-1,1] = train_mse[0], val_mse[0]

  15.         model.save(f'{base_path}epoch_{i}.h5')

  16. ​

  17.         for j in range(0,days):

  18.             sample = X_test[j,:,:].reshape(1,length,1)

  19.             val_sample_pre = scaler.inverse_transform(model.predict(sample))

  20.             val_forecast_1_day.iloc[j,i-1] = val_sample_pre[0,0]

  21.         loss.iloc[i-1,2] = mean_squared_error(df.iloc[-days:],

  22.                                                                      val_forecast_1_day[f'Epoch {i}'])

 1-3 - יצירת דאטה פריים עבור אכלוס ערכי פונקציית המחיר של סט האימון, סט הולידציה וסט הטסט 

         האמיתי (לא המנורמל), כתלות במספר ה-epoch.

 5-6 - יצירת דאטה פריים המאכלס את 18 המשוערכים כתלות במספר ה-epoch.

 10-12 - אימון המודל והכנסת סט הולידציה.

 נזכיר שוב שהמודל מתאמן לחזות חודש אחד קדימה ולא 18 חודשים קדימה.

 19 - model.predict - משערך את החודש הבא.

        scaler.inverse_transform - ממחזיר את המחיר מסקלת הנרמול לסקלה האמיתית שלו.

21-22 - חישוב ערכי ה-Mse עם הטסט עבור כל epoch.

  1.     fig1,ax1 = plt.subplots(figsize=(12,6))

  2.     ax1.plot(loss.index[:],loss.iloc[:,0],label='train')

  3.     ax1.plot(loss.index[:],loss.iloc[:,1],label='Val test') 

  4.     ax1.set_xlabel('Epoch')

  5.     ax1.set_ylabel('Mse')

  6.     ax1.set_title('Loss Function')

  7.     plt.legend()

  8.     plt.grid()

  9.     fig1.savefig(f'{base_path}loss_function.png')

loss_function.png

 מתמונת פונקציית המחיר של סט האימון והולידציה עבור כל epoch, ניתן להסיק את הדברים הבאים:

 א. יש חשיבות למספר ה-epochs שכן קיבלנו ירידה חדה בשגיאה בטווח 40-60 epoch.

 ב. ניתן לראות ששגיאת האימון שואפת ל-0, ומכאן זה עניין של צורך המשתמש האם להמשיך לאמן על 

     מנת לדייק יותר ברזולוציות הנמוכות של השגיאה.

  1.     import matplotlib.animation as ani

  2.     fig1,ax1 = plt.subplots(1,2,figsize=(12,6))

  3.     plt.subplots_adjust(bottom = 0.2, top = 0.9)

  4.     ax1[0].plot(loss.index[0],loss.iloc[0,0],label=loss.columns[0][0])

  5.     ax1[0].plot(loss.index[0],loss.iloc[0,1],label=loss.columns[1][0])

  6.     ax1[0].set_ylabel('Mse');  axes[0].set_xlabel('Epoch')

  7.     ax1[0].legend();           ax1[0].grid()

  8.     ax1[1].plot(df.index[-days:],df[-days:],color='blue',label='True Values')

  9.     line_1, =ax1[1].plot(df.index[-days:], val_forecast_1_day.iloc[:,0].values,

  10.                                       color='r', label='Prediction')

  11.     ax1[1].tick_params(axis='x', rotation=45)

  12.     ax1[1].set_ylabel('Millions of Dollars');   axes[1].set_xlabel('Date')

  13.     ax1[1].legend();                            ax1[1].grid()

  14.     

  15.     def buildmebarchart(u=int):

  16.         ax1[0].plot(loss.index[:u],loss.iloc[:u,0].values,color='b')

  17.         ax1[0].plot(loss.index[:u],loss.iloc[:u,1].values,color='orange')

  18.         l,v = loss.columns[0][0],loss.columns[1][0]

  19.         ax1[0].set_title(f'{l} = {loss.iloc[u,0].round(4)} , {v} = {loss.iloc[u,1].round(4)}')

  20.         line_1.set_data(df.index[-days:],val_forecast_1_day.iloc[:,u].values)

  21.         ax1[1].set_title(f'Rmse = {loss.iloc[u,2].round(0)}')

  22.     animator = ani.FuncAnimation(fig, buildmebarchart, frames = 500 ,interval = 50)

  23.     plt.show()

  24.     animator.save(f'{base_path}animation.gif')

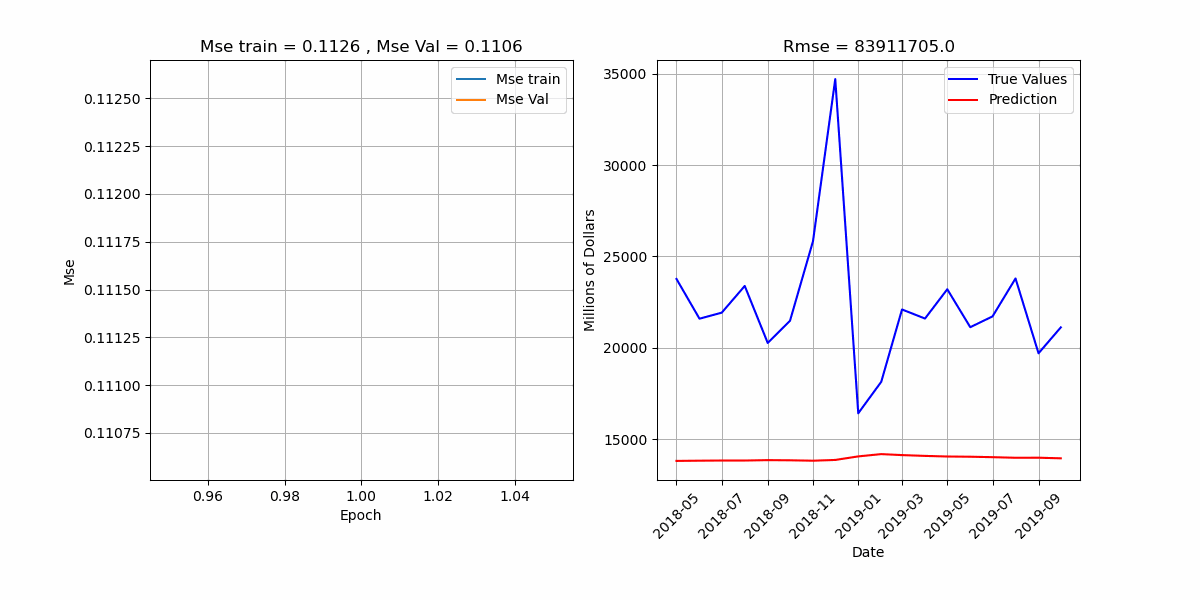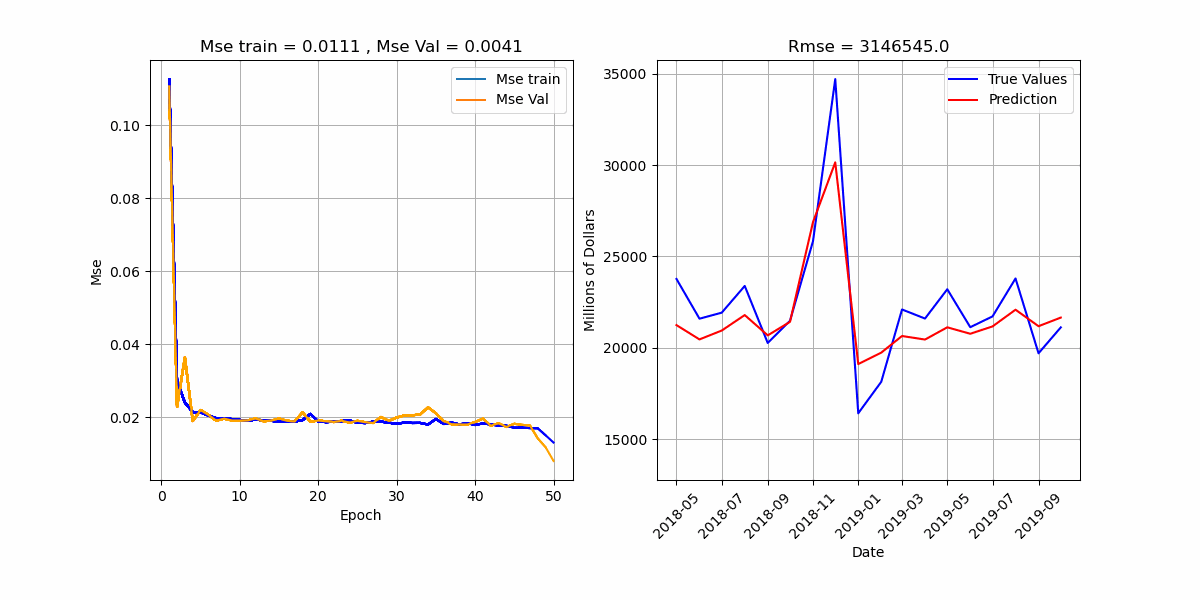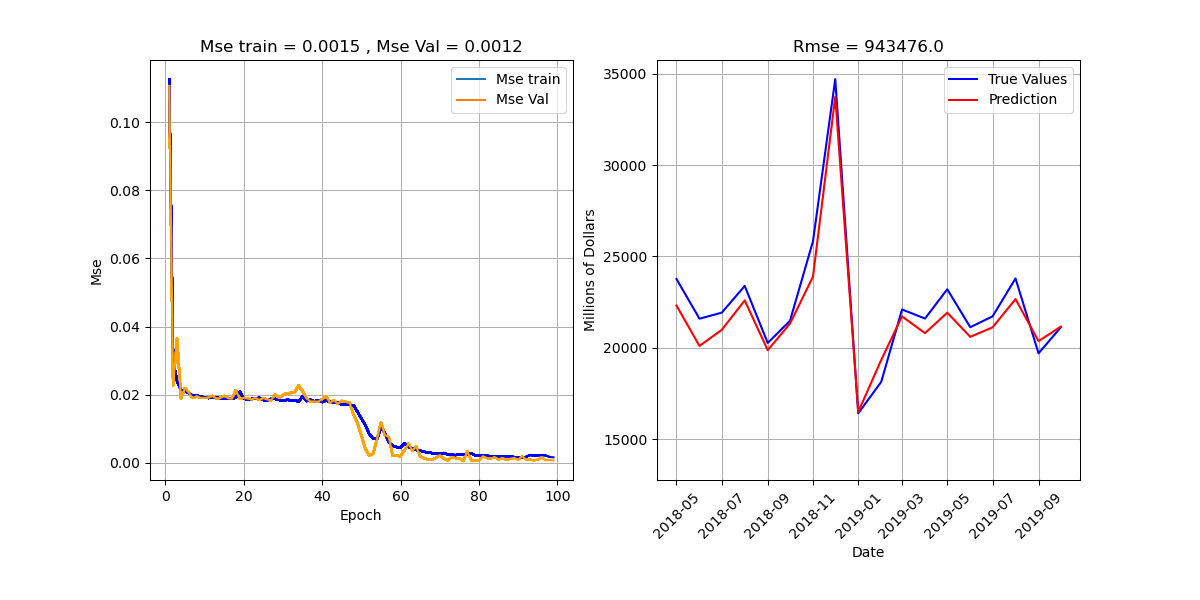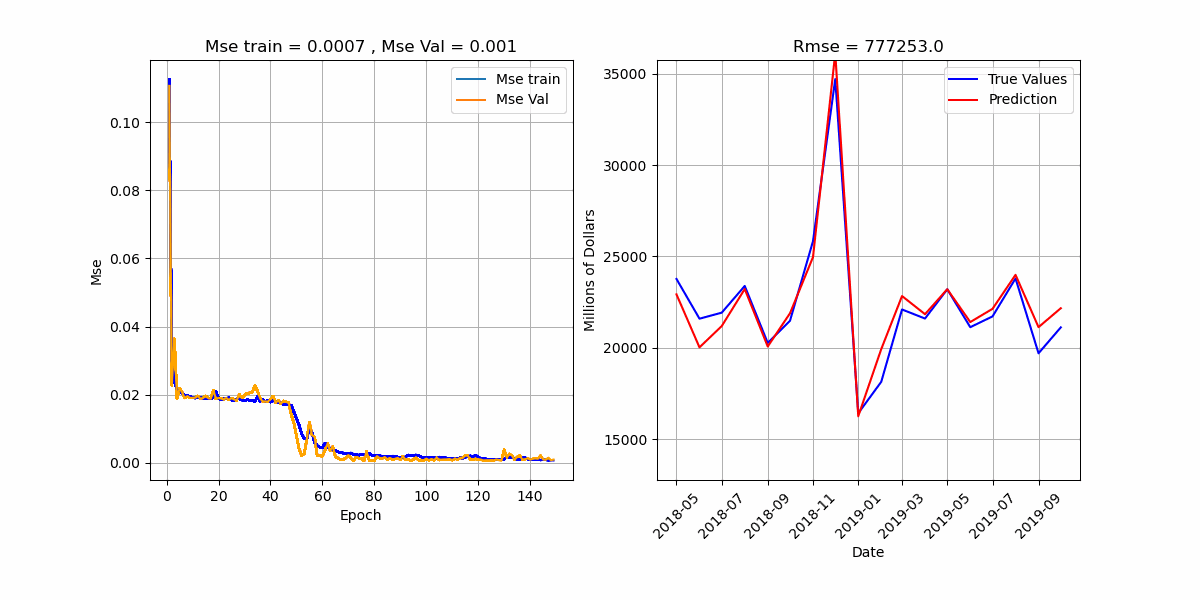
animation_6.gif

 סימולציה הממחישה את תהליך לימוד האלגוריתם. 

* בכותרת הגרף הימני מדובר ב-Mse ולא ב-Rmse.

  1.     min_mse_idx = loss.iloc[:,0].astype(float).idxmin()

  2. ​

  3.     from tensorflow import keras

  4.     final_model = keras.models.load_model(f'{base_path}epoch_{min_mse_idx}.h5')

  5. ​

  6.     result = df[-days:].copy()

  7.     result.columns = ['True Value']

  8. ​

  9.     prediction_1 =[]

  10.     for i in range(days):

  11.         sample = X_test[i,:,:].reshape(1,length,1)

  12.         val = scaler.inverse_transform(final_model.predict(sample))

  13.         prediction_1.append(val)

  14.     result['prediction_1'] = np.array(prediction_1)[:,0,0].astype(float)

  15. ​

  16.     prediction_2 =[]

  17.     current_batch = X_test[0,:,:].reshape(1,length,1)

  18.     for i in range(days):

  19.         current_prediction = final_model.predict(current_batch)[0]

  20.         prediction_2.append(current_prediction)

  21.         current_batch = np.append(current_batch[:,1:,:],[[current_prediction]],axis=1)

  22.     res = scaler.inverse_transform(prediction_2)

  23.     res = np.array(res)[:,0].astype(float)

  24.     result['prediction_2'] = res

 1. שמירת אינדקס ה-epoch בו סט האימון נתן את השגיאה המינימלית.

 2-3 - טעינת המודל עבור אינדקס זה.

 6-7 - יצירת דאטה פריים עבור התוצאות.

 9-14 - prediction 1  - אלו הם תוצאות החיזוי של חודש אחד בלבד קדימה עבור 18 חודשי הטסט.

 16-24 - prediction 2 - אלו הם תוצאות החיזוי עבור 18 חודשים קדימה מהחודש הנוכחי.

​

 ב-prediction 2 - תהליך השערוך מתבסס על חיזוי חודשים קודמים, כלומר עבור 36 חודשים האחרונים של סט האימון מתקבל שערוך החודש הבא, כעת על מנת לחזות את החודש אחריו נקח את החיזוי האחרון + 35 החודשים האחרונים מסט האימון ועל מנת לחזות את החודש השלישי נקח את שני החודשים שחזינו + 34 החודשים האחרונים מס האימון וכן הלאה וכן הלאה. 

 

ישנה גישה אחרת לחזות מספר דגימות קדימה כקבוצה, והיא

לבנות רשת שהמוצא שלה הוא מספר הדגימות שרוצים לחזות (במקרה כאן 18 חודשים) 

כלומר הרשת עצמה מתאמנת למוצא של 18 ניורונים.

  1.     rmse_prediction_1 = np.sqrt(mean_squared_error(result.iloc[:,0],

  2.                                                   result.iloc[:,1])).round(0)

  3.     rmse_prediction_2 = np.sqrt(mean_squared_error(result.iloc[:,0],

  4.                                                   result.iloc[:,2])).round(0)

  5.     rmse_mean_ratio_1 = (rmse_prediction_1/result.iloc[:,1].mean()).round(3)

  6.     rmse_mean_ratio_2 = (rmse_prediction_2/result.iloc[:,2].mean()).round(3)

 1-4 - חישוב Rmse עבור כל אחת מהתחזיות.

 5-6 - חישוב היחס בין Rmse לבין ממוצע חודשי הטסט.

         חישוב זה יכול לתת אומדן האם התוצאות מספיק מדוייקת. 

  1.     fig3,ax3 = plt.subplots(figsize=(12,6))

  2.     ax3.plot(result.index[:],result[:,0],label='True Value')

  3.     ax3.plot(result.index[:],result[:,1],label=f'Prediction 1.   rmse = {rmse_prediction_1}'')

  4.     ax3.plot(result.index[:],result[:,2],label=f'Prediction 2.   rmse = {rmse_prediction_2}'')

  5.     ax3.set_xlabel('Date')

  6.     ax3.set_ylabel('Millions of Dollars')

  7.     ax3.set_title('Forecast Data')

  8.     plt.legend()

  9.     plt.grid()

  10.     fig3.savefig(f'{base_path}Forecast.png'

Forecast.png

בתמונה ניתן לראות את התוצאות הסופיות עבור כל אחת מהתחזיות, כמו כן נראה שהתקבל Rmse

נמוך יותר עבור התחזית של החודש אחד בלבד קדימה, מה שהגיוני סה"כ אבל לא כלכך משמעותי ביחס  לשגיאה של התחזית על סמך התחזית.

כמו כן ניתן לראות שהיחס בין השגיאה לממוצע הוא הבדל של שני סדרי גודל כך שבעיניי זה דיוק יפה

אך עם זאת ניתן להגיע לדיוקים הרבה יותר גבוהים במיוחד שהדאטה סט הוא כלכך ידידותי במקרה זה.

bottom of page